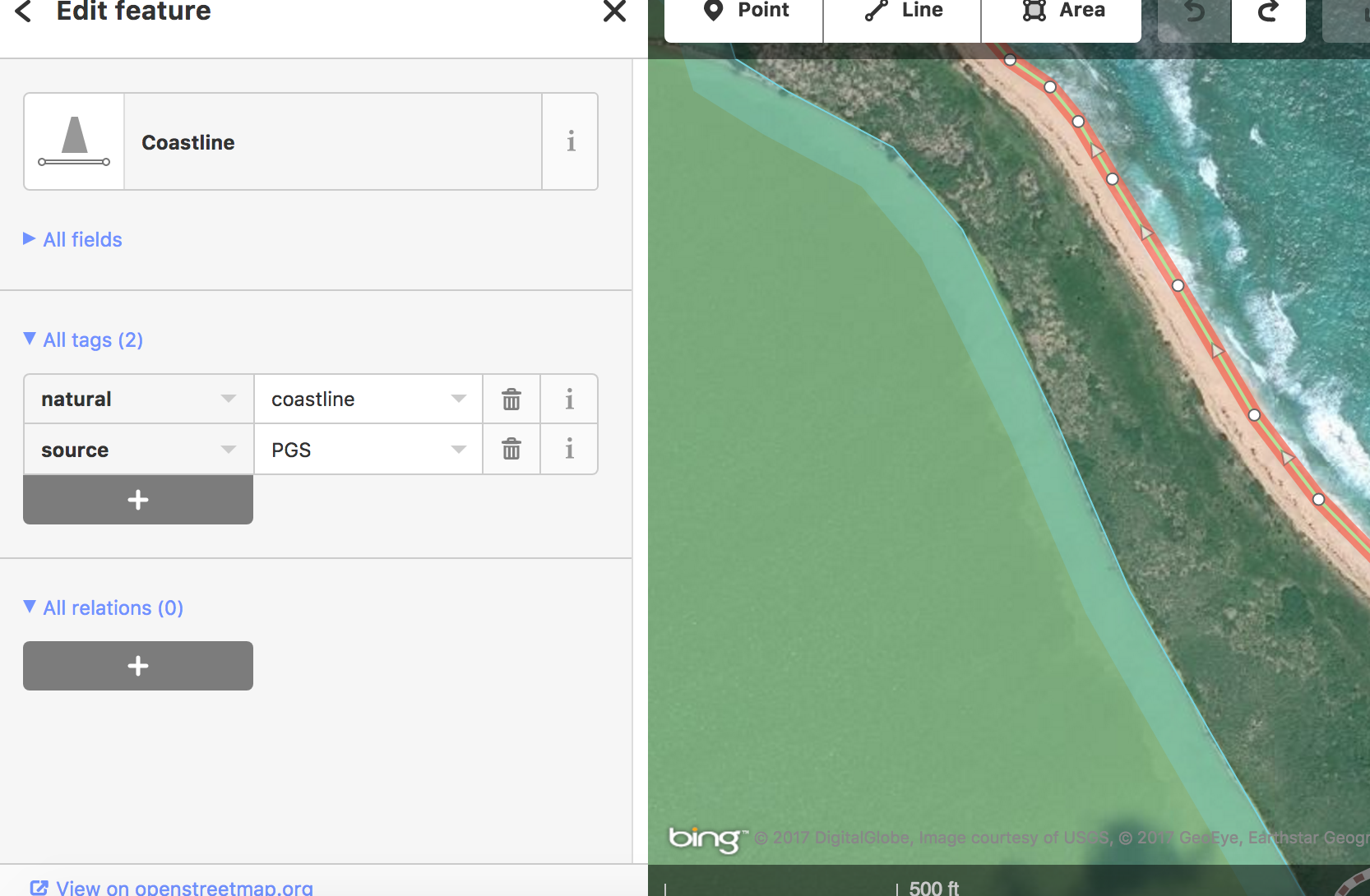
I'm a newbie iD editor, but I dove in to try to figure out what's going on. I found that islands that extracted properly have a relation defined between their coastline (line) feature and their island feature, in which the coastline is defined as the "outer" of the island. On the other hand, islands that didn't extract properly had a coastline tag, but no island tag. My question is how to define the area of an island as an island feature, and how to create the required relation between that and the coastline feature, for the islands that need this. Does a guide or tutorial exist for doing this task in iD? I have looked and haven't been able to find one. EDIT: I added two images to show what I'm finding. The first shows tags for the coastline of Long Island in The Bahamas, where the coastline is tagged as having a relation with the island. The second is for the coastline of the island of Eleuthera in The Bahamas, where no island tag exists.
asked 16 Apr '17, 06:15 abijah edited 16 Apr '17, 13:29 |
2 Answers:
I would think that a relation in the sense that osm uses would not be required unless you want to group a number of islands under the same name or the island is very large. Can't help with iD but JOSM seems well suited for multipolygon mapping. answered 16 Apr '17, 06:41 nevw edited 16 Apr '17, 07:07 |
The solution is to create a relation and give it these tags: Then add all the parts of coastline that makes up the coastline for the island. I found that to do this in ID was not so easy so the easiest way to do this and my advice to you is to install JOSM, have a quick view at this instructional movie for how to do this. It's in Russian and quite dated, but he presses the same buttons and they still look the same. Or, a quick fix, if you don't want to figure it out. Put a note on the map explaining what's wrong and someone will/might fix it. Edit: Some examples of a medium island and a large island with lots of ways that form the outer way that makes the coastline of the island. answered 16 Apr '17, 14:10 FredrikLindseth edited 16 Apr '17, 14:16 |

 While trying to perform an extract of Caribbean islands in Quick OSM (Overpass API), I discovered that some major islands were left out of my extract. I supposed that the problem was inconsistent tagging.
While trying to perform an extract of Caribbean islands in Quick OSM (Overpass API), I discovered that some major islands were left out of my extract. I supposed that the problem was inconsistent tagging.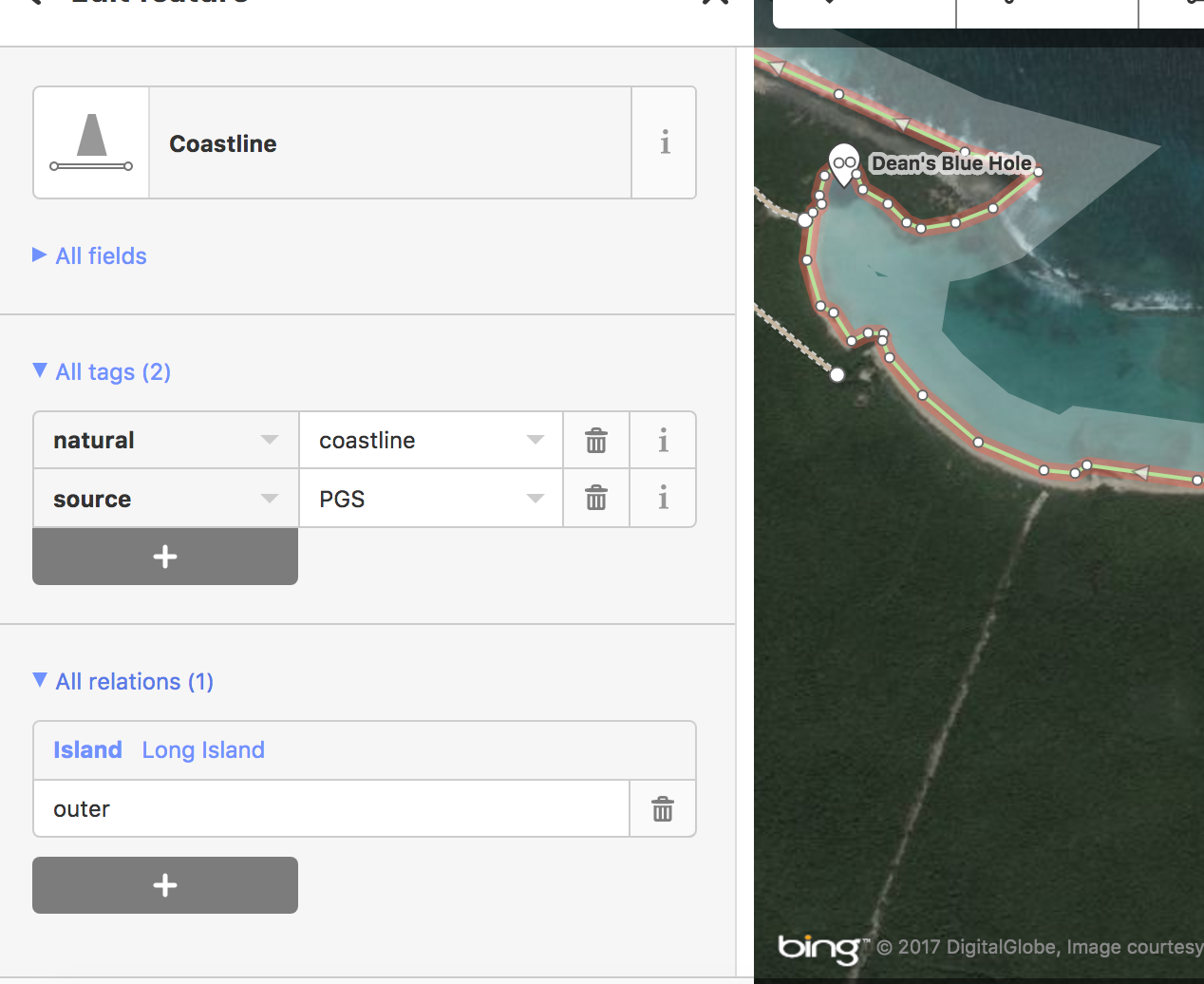 Many thanks in advance!
Many thanks in advance!
I added some images to the original post to explain what I'm seeing. How can I use the coastline features to create island features?